The Dorian scale is one of the most widely recognized and utilized musical scales, yet its deeper mathematical and theoretical significance remains a mystery to most. At its core, the Dorian scale is familiar to musicians and composers in several formats:
As a sequence of pitches: D, E, F, G, A, B, C, D;
As an intervallic formula: whole step (ws) - half step (hs) - ws - ws - ws - hs - ws;
Numerically: [0, 2, 3, 5, 7, 9, 10, 0] (octave-inclusive); or
As a sequence of Roman numerals: II, III, IV, V, VI, VII, I.
While many view the Dorian scale as the second mode (II) of the Ionian (major) scale (I), this conventional classification stems from centuries of tradition rather than an objective musical hierarchy. The Dorian scale is the first scale to emerge from the Circle of Fifths, making it arguably the most fundamental of all heptatonic scales.
A Case for Dorian as the First Mode
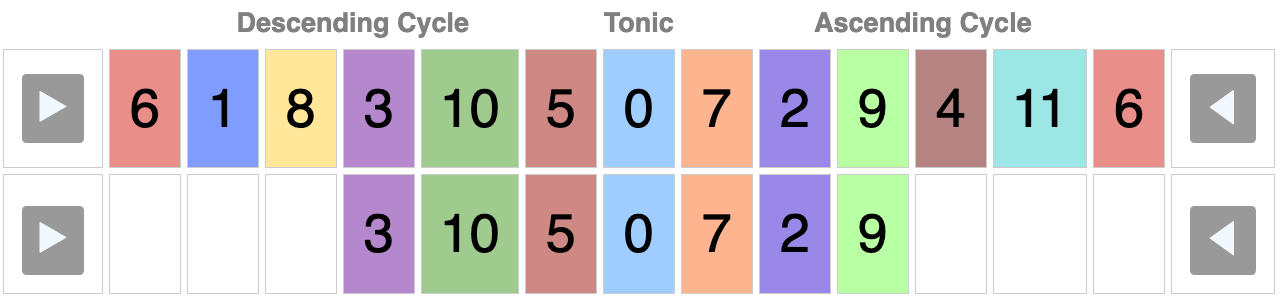
Western music education typically places the Ionian scale at the forefront, designating Dorian as a subordinate “minor” mode. This ordering was shaped by historical conventions, such as the modal theory of medieval monks and the codifications of twentieth-century music schools. However, a closer examination of the Circle of Fifths reveals that the Dorian scale forms naturally and symmetrically by combining the first three ascending and descending perfect fifths from a tonic:
Ascending: D → A → E → B or [0 → 7 → 2 → 9]
Descending: D → G → C → F or [0 → 5 → 10 → 3]
This symmetry establishes the Dorian scale as the logical starting point for modal systems, preceding the other six asymmetrical modes:
Dorian (I) – [0, 2, 3, 5, 7, 9, 10]
Phrygian (II) – [2, 3, 5, 7, 9, 10, 0]
Lydian (III) – [3, 5, 7, 9, 10, 0, 2]
Mixolydian (IV) – [5, 7, 9, 10, 0, 2, 3]
Aeolian (V) – [7, 9, 10, 0, 2, 3, 5]
Locrian (VI) – [9, 10, 0, 2, 3, 5, 7]
Ionian (VII) – [10, 0, 2, 3, 5, 7, 9]
Rotations, Reflections, and Permutations
The versatility of the Dorian scale extends far beyond its symmetrical construction. Applying modal rotations and inversions (reflections) reveals a staggering number of permutations, enabling nearly infinite creative potential.
Modal Rotations (6 Ascending and 6 Descending Orders)
By rotating the pitches, we derive six unique ascending and descending sequences (modes), each retaining the essential Dorian character.
Ascending modes:
[0, 2, 3, 5, 7, 9, 10]
[2, 3, 5, 7, 9, 10, 0]
[3, 5, 7, 9, 10, 0, 2]
[5, 7, 9, 10, 0, 2, 3]
[7, 9, 10, 0, 2, 3, 5]
[9, 10, 0, 2, 3, 5, 7]
[10, 0, 2, 3, 5, 7, 9]
Descending modes:
[0, 10, 9, 7, 5, 3, 2]
[10, 9, 7, 5, 3, 2, 0]
[9, 7, 5, 3, 2, 0, 10]
[7, 5, 3, 2, 0, 10, 9]
[5, 3, 2, 0, 10, 9, 7]
[3, 2, 0, 10, 9, 7, 5]
[2, 0, 10, 9, 7, 5, 3]
Reflections (12 Inversions)
The Dorian scale’s intervals can also be reflected around 12 axes to produce inversions. These reflections transpose the tonic and alter scale contour, producing 12 the Dorian scales, one for each tonic.
[0, 2, 3, 5, 7, 9, 10] (axis: 0-6, prime)
[1, 11, 10, 8, 6, 4, 3] (axis: 0.5-6.5)
[2, 0, 11, 9, 7, 5, 4] (axis: 1-7)
[3, 1, 0, 10, 8, 6, 4] (axis: 1.5-7.5)
[4, 2, 1, 11, 9, 7, 6] (axis: 2-8)
[5, 3, 2, 0, 10, 8, 7] (axis: 2.5-8.5)
[6, 4, 3, 1, 11, 9, 8] (axis: 3-9)
[7, 5, 4, 2, 0, 10, 9] (axis: 3.5-9.5)
[8, 6, 5, 3, 1, 11, 10] (axis: 4-10)
[9, 7, 6, 4, 2, 0, 11] (axis: 4.5-10.5)
[10, 8, 7, 5, 3, 1, 0] (axis: 5-11)
[11, 9, 8, 6, 4, 2, 1] (axis: 5.5-11.5)
The Dorian Chord
Stacking two triads above the tonic produces a Dorian chord. Inverting the two triads individually, produces all possible arrangements for the chord. Below are 6 of the 36 voicings for the Dorian chord.
[0] → [3, 7, 10] → [2, 5, 9]
[0] → [3, 10, 7] → [2, 9, 5]
[0] → [7, 3, 10] → [5, 2, 9]
[0] → [7, 10, 3] → [5, 9, 2]
[0] → [10, 3, 7] → [9, 2, 5]
[0] → [10, 7, 3] → [9, 5, 2]
With 5,040 permutations for each Dorian scale, the combinatorial potential is enormous.
Dorian Chromatic Chord
Stacking the remaining 5 notes (pentatonic scale) above the Dorian chord, increases the harmonic density from 7 to 12 notes, producing a Dorian chromatic chord.
[0] → [3, 7, 10] → [2, 5, 9] → [11, 1, 4, 6, 8]
There are 4,320 possible variations for this Dorian chromatic chord.
Why This Matters
The Dorian scale’s mathematical elegance and symmetrical construction challenge traditional Western music pedagogy, which often limits its role to a secondary “minor” scale. Recognizing Dorian as a foundational scale invites fresh perspectives for composition and improvisation, allowing musicians to explore the vast permutations and harmonic possibilities it offers.
By revisiting these traditional scales with modern tools and open minds, we can expand the boundaries of musical creativity and innovation. After all, the “rules of music” are meant to be flexible, serving as guides rather than constraints.
Conclusion
The Dorian scale is not merely a secondary mode—it is a cornerstone of Western music theory, brimming with untapped potential. From its natural harmonic emergence from the Circle of Fifths to its diverse permutations, the Dorian scale proves that even the most familiar musical structures can yield nearly infinite possibilities when viewed through a new lens of pure mathematics.
This exploration is not just theoretical; it’s a call to action for musicians, educators, and theorists to embrace flexibility, challenge tradition, and unlock new dimensions of musical expression.
For a more detailed explanation of the math behind the Harken Music system, see, “The Math Behind The Music” and “Reimagining Musical Harmony”, by Mitch Kahle.
Please try our free open-source proof-of-concept demo* at harkenmusic.com, where you can choose any combination size (from 1 to 12 notes) from the pull-down menu; then select any particular combination from the numbered list, to see and hear all the permutations, reflections (inversions), and rotations (transpositions).
*Note: a desktop or laptop computer and current web browser (Chrome, Safari, etc.) are required for using the demo; however there are no downloads, sign-up, or subscription requirements. Enjoy!
This information and related open-source software code are available on Harken Music and Github as open-source software under the standard MIT License set forth below.
Copyright 2024 Mitchell Kahle and Holly J. Huber
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the “Software”), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.