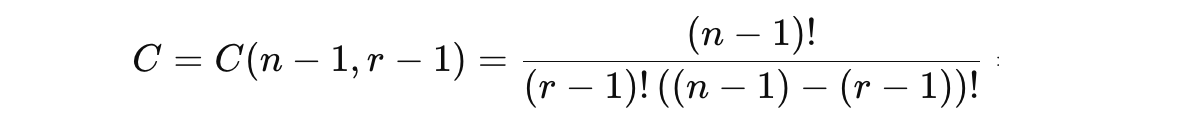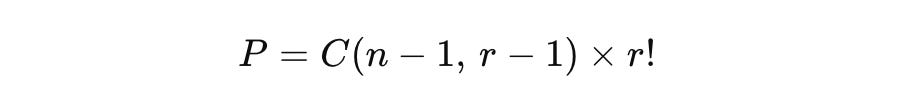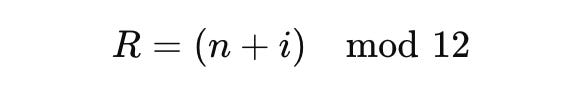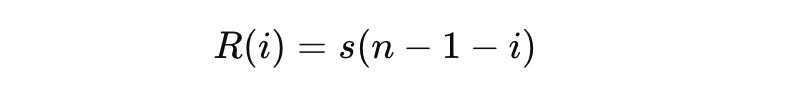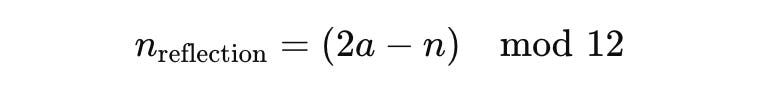The Five Formulas for Harmony

These Five Simple Formulas Calculate All Of 12-Tone Equal Temperament

Mitch Kahle

Dec 15, 2024

Adjustment for Fixed Tonic: The fixed tonic 0 is required in all combinations and accounted for using n = n − 1 and r = r − 1 in the formula above.
Variables:
- C = Number of combinations for size r
- n: Total notes (n = 12 reduced to n − 1 = 11 to account for fixed tonic)
- r: Combination size (r = 12 from 1 to 11, r = r − 1 to account for fixed tonic)
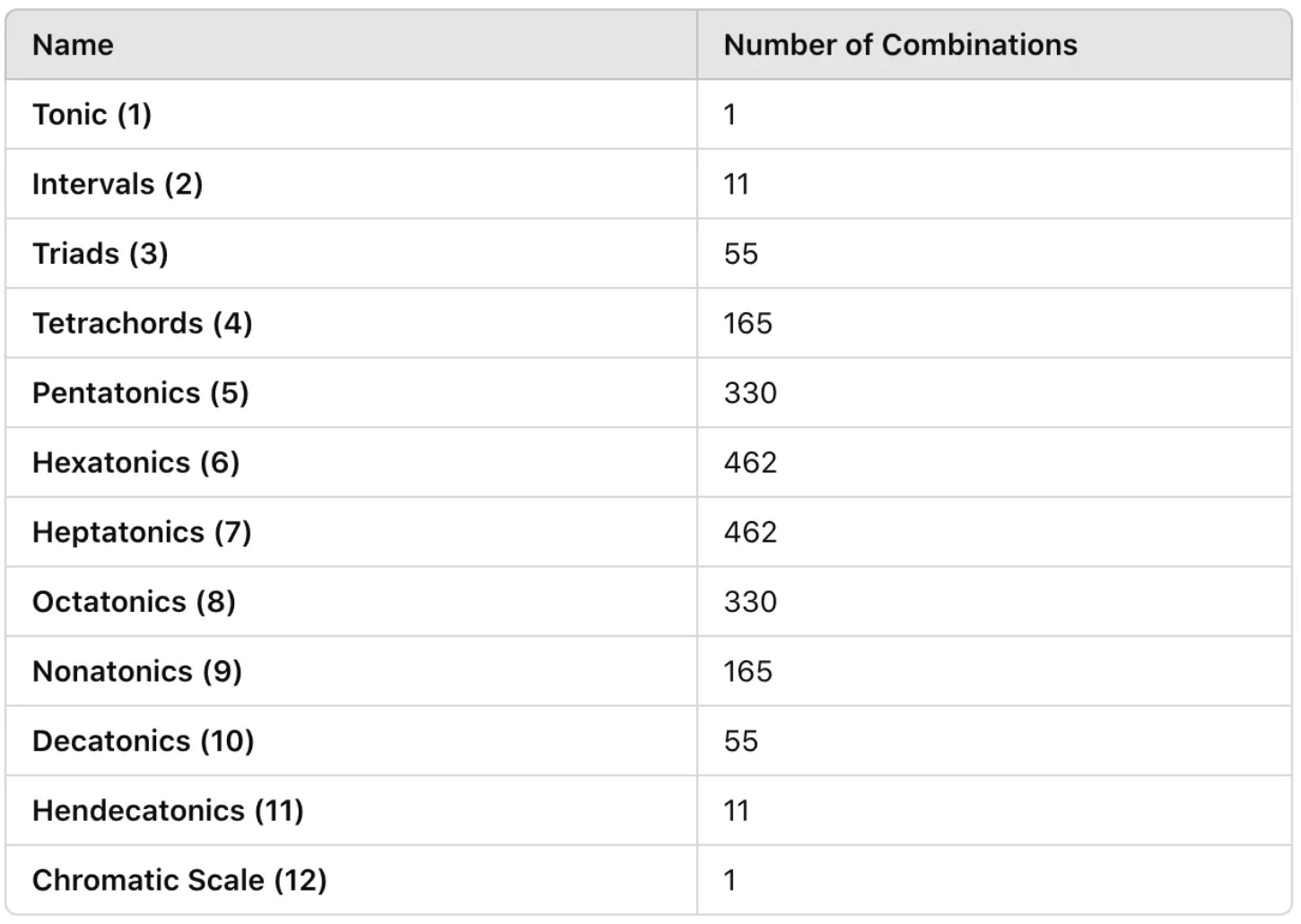
Example solution applying the formula above: C = (n = 12, r = 5) = 330

Table of Combinations (combination sizes 1-12)

Permutations

The fixed tonic 0 must be included in all permutations and accounted for using n = n − 1 and r = r − 1 in the formula above.
Variables:
- P = Number of permutations of combination
- n: Total notes (n = 12 reduced to n − 1 = 11 to account for the fixed tonic)
- r: Combination size (r = 12 from 1 to 11, r = r − 1 to account for the fixed tonic)
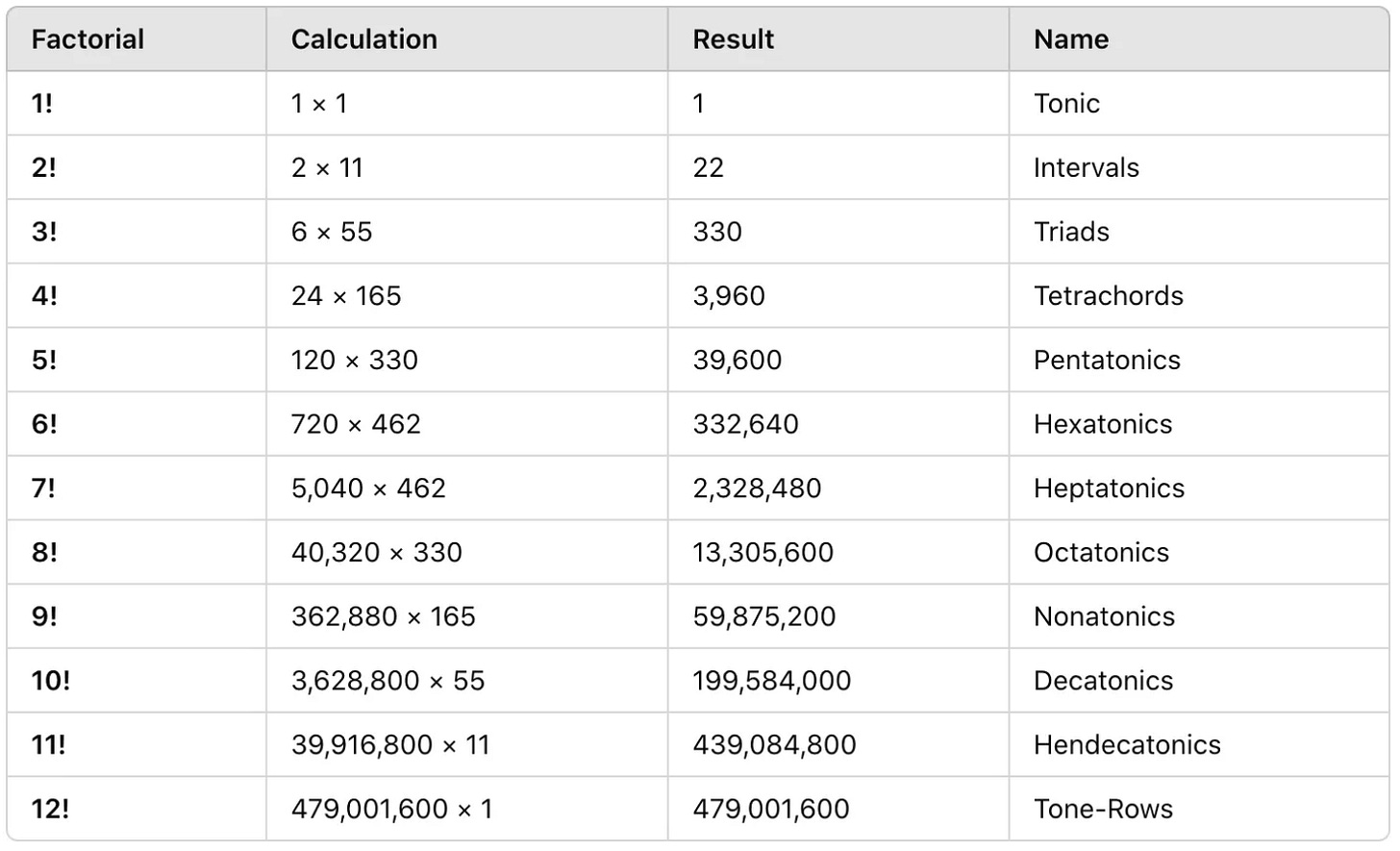
Example solution applying the formula above: P = (n = 12, r = 5, C = 330) = 39,600

Table of Permutations (combination sizes 1-12)

Rotations (Modes)

Variables:
- R: Rotated note at position i
- n: note to be rotated
- i: interval offset
First determine the interval i by comparing a resulting pitch class r to the original note n.
- i = (r - n) mod 12,
- Once you have i, you can then apply it in the rotations formula above.

Retrogrades (Directions)

Variables:
- r_i: Retrograded note
- s: Original sequence

Reflections (Inversions)

Variables:
- n_reflection: Reflected note
- n: Note being reflected
- a: Reflection axis

Summary

By applying these five simple formulas and explicitly adjusting for the fixed tonic (0) where required, we can generate all combinations, arrangements, and transformations possible in 12-tone equal temperament.

For a more detailed explanation of this and all the math used in creating the Harken Music system, please read: “The Math Behind The Music” and “The Future of Music is Math” by Mitch Kahle.

See also: “Harken Music: A New Mathematical Framework for 12-Tone Harmony”, by ChatGPT 4o, and for an even deeper dive into the power of mathematics, read Factorials and Fractions “Navigating the 12-tone matrix,” by Mitch Kahle.

Please try our open-source proof-of-concept demo* at harkenmusic.com, where you can choose any combination size (from 1 to 12 notes) from the pull-down menu; then select any particular combination from the numbered list, to see and hear all the permutations, reflections (inversions), and rotations (transpositions).

*Note: a desktop or laptop computer and current web browser (Chrome, Safari, etc.) are required for using the demo; however there are no downloads, sign-up, or subscription requirements.

It cannot be overstated that the Harken Music system uses only mathematics and math related programming code. The programming does not include or use any databases, lookup tables, or other sources of data. Everything—nearly 1.2 billion musical combinations and permutations—is calculated on the fly.

This information and related software code are available on Harken Music and Github as open-source software under the standard MIT License set forth below.

Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the “Software”), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:

The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.

***

Harken Music